Neste artigo serão abordados os conceitos básicos de álgebra relacional. Esta que está por trás de consultas relacionadas a bancos de dados relacionais. A linguagem SQL foi criada a partir da álgebra relacional e por isso ter uma noção básica dos seu conceitos se torna muito importante.
Operações Básicas
Seleção: σ
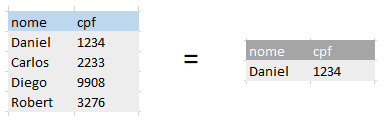
A seleção, como o próprio nome já diz, seleciona linhas, tuplas por meio de uma determinada condição.
Ex: σnome=“Daniel”(cliente)
Projeção: π
A projeção é utilizada quando existe a necessidade de pegar somente colunas de interesse em uma relação, e não trabalhar com todas as colunas dessa relação.
Ex: πnome(cliente)
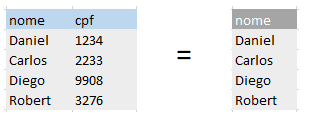
União: ⋃
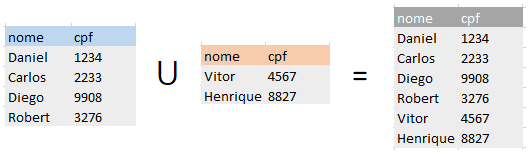
A união entre duas relações AUB, traz em uma nova relação C com todas as tuplas existentes em A e B, sem repetição de tupla.
Ex: (clientesA) ⋃ (clientesB)
Interseção: ∩
A interseção de duas relações A∩B traz uma nova relação C contendo as tuplas, linhas em comum, ou seja, que existam nas duas relações.
Ex: (clientesA) ∩ (clientesC)

Diferença de conjuntos: −
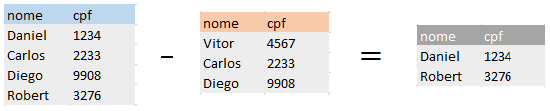
A diferença entre duas relações A – B, traz uma nova relação C com tuplas que existem em A mas não existem em B, ou seja, que só existem em A. Do mesmo, equivale para B – A, traz uma nova relação com as tuplas que só existem em B, portanto, a ordem é importante.
Ex: (clientesA) − (clientesC)
Produto cartesiano: ×
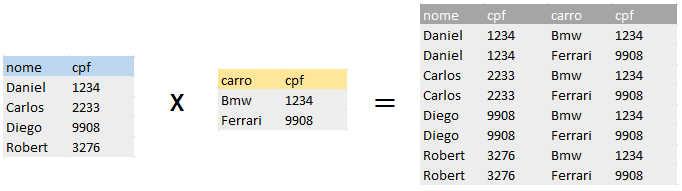
O produto cartesiano entre duas relações A X B traz uma nova relação C que contém todos os campos, colunas que A e B contém, e a combinação de cada tupla de A com cada tupla em B.
Ex: (cliente) x (veiculo)
Outras operações
Junção: ⋈
Logo após a realização de um produto cartesiano em uma relação, geralmente existe a necessidade de se fazer uma seleção na qual os campos que estão em A e também estão em B sejam iguais, porque o produto cartesiano traz tuplas que não são de interesse. A junção é a operação que simplifica tudo isso. Ela realiza um produto cartesiano, depois uma seleção das tuplas de interesse e por fim uma projeção, para remoção de colunas duplicadas.
Ex: (cliente) ⋈ (veiculo)

Divisão: ÷
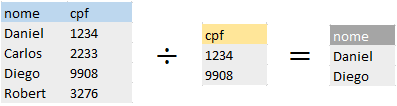
A operação de divisão entre duas relações A ÷ B traz uma nova relação C com todas as tuplas que possuem campos em comum nas duas relações.
Ex: (cliente) ÷ (cpfProcurado)
Renomeação: ρ
A renomeação, de maneira intuitiva, permite renomear uma relação, chamar por mais de um nome, e também nomear uma operação em cima de uma relação, por exemplo, nomear o resultado da projeção em uma relação A.
Atribuição: ← EX: X ← (A × B)
A atribuição permite expressar consultas de uma maneira simples, de forma a ser possível trabalhar com estas.
Funções e Operações agregadas
As operações agregadas foram criadas para simplificar as consultas ás relações, de forma que algumas funções que são comumente utilizadas sejam facilmente acessadas.
avg: valor médio
min: valor mínimo
max: valor máximo
sum: soma dos valores
count: quantidade de um determinado valor
As operações agregadas são representadas por um Γ da seguinte maneira:
Γoperação_de_agregação (nome_da_coluna)(nome_da_relação)
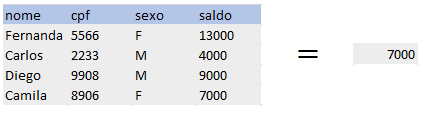
EX: Γmin (saldo)(Conta)
Você também pode aplicar essas operações de forma agrupada em relações:
(nome_do_campo_agrupado)Γoperação_de_agregação (nome_da_coluna)(nome_da_relação)
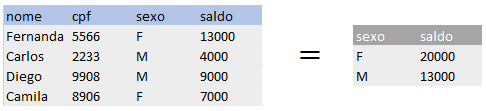
EX: (sexo)Γsum (saldo)(Conta)
Conclusão
Neste post foram vistos os principais recursos da álgebra relacional para manipulação de dados. Fica para próximos posts as funções para inserção, remoção e atualização. Também a relação entre a linguagem SQL e a Álgebra relacional. Até a próxima.

3 comentários
Wellington dos Santos Teixeira · 03/07/2019 às 00:21
Muito bom, esclareceu todas as minhas dúvidas. Obrigado!!!
Rafael · 14/05/2022 às 22:37
Olá, vale ressaltar que a explicação sobre divisão está equivocada. No caso a divisão retorna as tuplas que possuem TODOS os casos correspondentes da segunda tabela, no exemplo em questão não será retornada nenhuma relação.
Um exemplo correto para dar o retorno do exemplo é:
table =
{
nome:string, cpf:number
Daniel, 1234
Daniel, 9908
Carlos, 2233
Diego, 9908
Diego, 1234
Robert, 3276
}
table2 =
{
cpf:number
1234
9908
}
Henry · 06/09/2023 às 17:31
Exatamente. Também percebi esse erro claramente. Na divisão sempre a noção de “todos” está envolvida.